Welcome! I am Nachiket, a rising 5th-year PhD candidate in the Department of Physics at Boston University. My research is focused on the intersection of chaos theory, nonlinear dynamics, and statistical mechanics. On this site, you will find an overview of my research projects, publications, talks, and my CV.

Projects

Probing Chaos in Classical and Quantum Systems

In everyday physics, we often describe a system as “chaotic” if it exhibits the famous “butterfly effect” – where a tiny, almost unnoticeable change in its starting conditions leads to dramatically different outcomes. This definition, however, completely breaks down in the quantum realm. Quantum mechanics is a linear theory, so the classic butterfly effect is impossible. For decades, physicists worked around this by defining a quantum system as chaotic only if its classical counterpart is chaotic. They have looked for signatures of this chaos in the distribution of the quantum system’s energy levels.

More recently, however, works by Pandey et al. and Lim et al. have established a new way to connect these two realms. They have shown that both classical and quantum chaos can be universally defined by a different kind of sensitivity: to adiabatic changes in the system. This provides a unified language to describe chaos, defining it as how any system reacts to slow, subtle changes.

Our work reconciles these two different views of chaos. We have shown that the classic butterfly effect and this newer concept of sensitivity to adiabatic deformations are actually two sides of the same coin. At a fundamental level, both result in a “diffusion” of observables. We can measure the rate of this diffusion using a tool we call the “observable drift”. Since this method reveals the same underlying diffusion process for both definitions, we have demonstrated that they are not two separate ideas, but rather the same essential phenomenon viewed from different perspectives.

The Fermi–Pasta–Ulam–Tsingou Problem

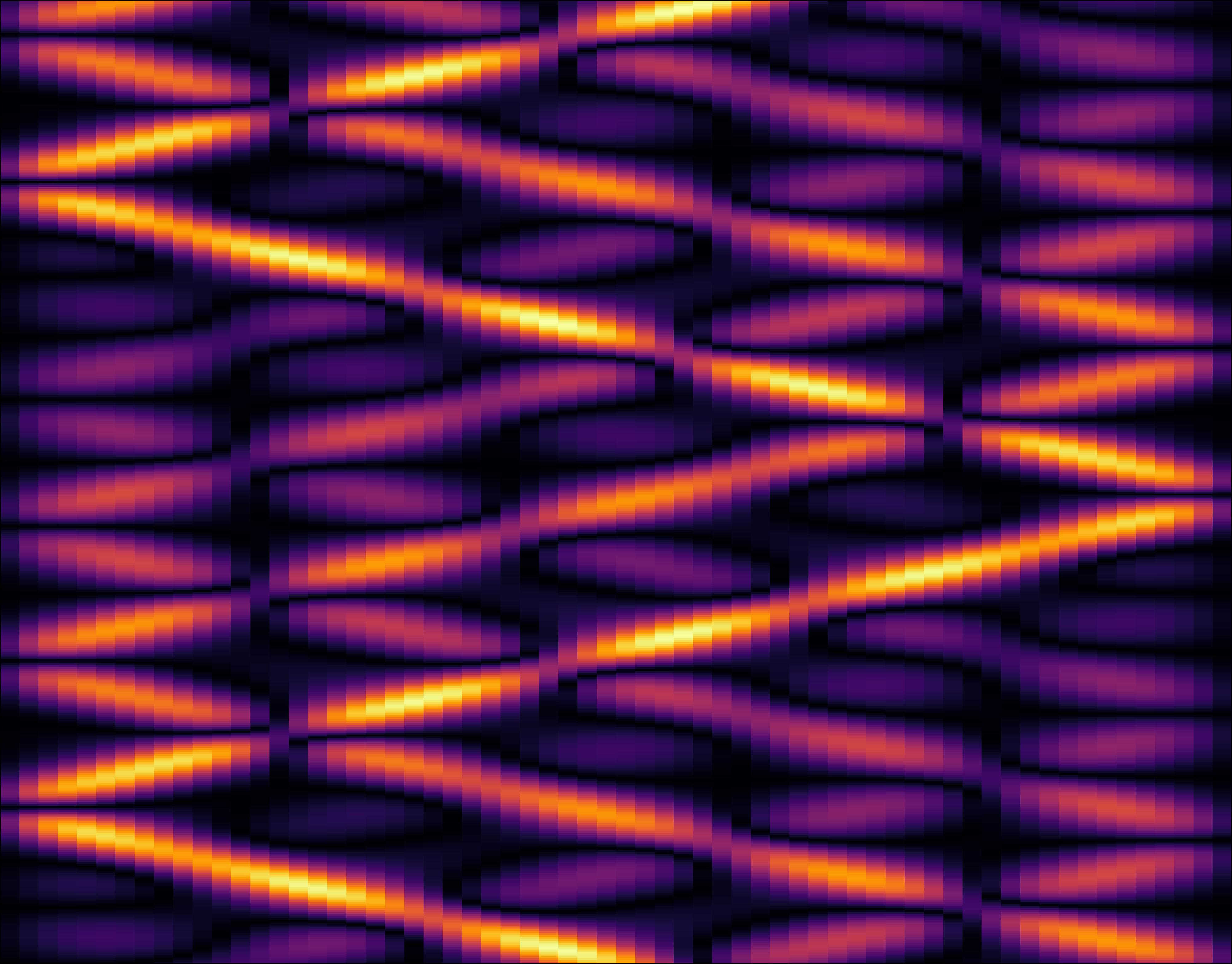
The Fermi-Pasta-Ulam-Tsingou (FPUT) problem studies a simple, one-dimensional chain of interacting particles. In a landmark 1953 computer experiment, researchers expected that energy given to the system would quickly spread out evenly among all its modes, resulting in the thermalization of the system. Instead, they observed that the energy periodically returned to its initial state, a surprising phenomenon known as FPUT recurrence.

After over 50 years of study, it is now understood that the system first gets trapped in a long-lasting, stable configuration called the “metastable state” before eventually thermalizing. Our work investigates the role of specific periodic states within the system known as q-breathers, where energy remains localized to a small number of modes. We have observed that the system’s metastable state is actually a nonlinear superposition of these individual q-breathers. By studying resonances between these breathers, we can understand the mechanism that eventually destabilizes this metastable state and leads to true thermal equilibrium.